CSE 5311 Section 501 Fall 1998
Homework 7
Due: May 6, 1998, in class

1. Compute the product of the polynomials A(x) = and B(x) = using the method described in class.

   w(0,8) = 1.000000 + 0.000000i
   w(1,8) = 0.707107 + 0.707107i
   w(2,8) = 0.000000 + 1.000000i
   w(3,8) = -0.707107 + 0.707107i
   w(4,8) = -1.000000 + 0.000000i
   w(5,8) = -0.707107 + -0.707107i
   w(6,8) = 0.000000 + -1.000000i
   w(7,8) = 0.707107 + -0.707107i
   FFT(A) = (-3 #C(-14.242640687119284 4.6568542494923806)
             #C(-9.0000000000000018 -6.0)
             #C(-5.7573593128807135 6.6568542494923788) -19
             #C(-5.7573593128807161 -6.6568542494923806)
             #C(-8.9999999999999982 6.0)
             #C(-14.242640687119287 -4.6568542494923788))
   FFT(B) = (5 #C(-6.8994949366116636 1.4142135623730967)
             #C(2.9999999999999969 -14.0)
             #C(12.899494936611667 1.4142135623730923) 1
             #C(12.899494936611664 -1.4142135623730967)
             #C(3.0000000000000031 14.0)
             #C(-6.8994949366116671 -1.4142135623730923))
   point-value C = (-15 #C(91.681240867131862 -52.272077938642163)
                    #C(-110.99999999999997 108.00000000000004)
                    #C(-83.681240867131862 77.727922061357859) -19
                    #C(-83.681240867131905 -77.72792206135783)
                    #C(-111.00000000000003 -107.99999999999996)
                    #C(91.681240867131947 52.272077938642106))
   coefficient C = (#C(-29.999999999999993 7.1054273576010019E-15)
                    #C(63.0 -5.4522087799407926E-15)
                    #C(-9.0 -1.8873791418627661E-15)
                    #C(-53.0 9.0049224587412935E-15)
                    #C(-34.000000000000007 1.4210854715202004E-14)
                    #C(-8.0 -5.4522087799407926E-15)
                    #C(56.0 -1.9428902930940239E-14)
                    #C(0.0 1.8994951011402916E-15))

2. In the on-line convex-hull problem, we are given the set Q of n points, one point at a time. After receiving each point, we are to compute the convex hull of the points seen so far. Obviously, we could run Graham's scan once for each point, with a total running time of . Show how to solve the on-line convex-hull problem in a total of time.

   This implementation of the on-line convex-hull problem first determines if the new point p is inside the current convex hull (ordered counter-clockwise) by checking for left turns on each angle . If no such left turns are found, the new point is inside the current convex hull and can be discarded. Since left turns can be checked in constant time, the entire check takes O(n) worst case.

   If a left turn is found, then the new point p is outside the convex hull. From the new point p, we then compute the two points and on the convex hull having the smallest and largest (respectively) polar angle with respect to p. This can be done in worst case O(n) time. Then, we remove the points on the convex hull between and (in increasing counter-clockwise order from ) and replace them with p. This step is also O(n) worst case.

   Therefore, each point requires worst case O(n) processing, so that the total running time for all n points is .

3. Consider the bin-packing problem in which we are given n objects having sizes , and we want to pack the objects into a minimum number of unit-sized bins, each holding a total size not exceeding 1 (this is Problem 37-1 in the textbook).

   a.

   Prove that the problem of determining the minimum number of bins required is NP-hard. (Hint: reduce from the subset-sum problem).

   We can prove the bin-packing problem is NP-Hard by converting it to a decision problem (BP) and reducing the NP-Complete subset-sum problem (SS) to a specialization of the bin-packing decision problem. Here are the two decision problems.

    
   		SS =    there exists    such that   
   
   		 BP =    all objects in   
   can be placed in k or fewer bins    
   

   Since the bin-packing problem does not constrain how full the bins are, one specialization of the bin-packing problem, spec(BP), would be to constrain at least one bin to be exactly full.

    
   		 spec(BP) =    āll objects in   
   can be placed in k or fewer bins
   
   				 at least one of which is exactly full    
   

   Since SS is NP-Complete, showing SS 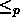spec(BP) implies that BP is NP-Hard. The reduction algorithm first removes all integers from 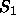that are greater than t. Let the remaining integers be 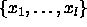. We then call spec(BP) with l objects whose sizes are 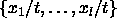, and k=l. This is a polynomial-time reduction.

   To prove this reduction is valid, note that if some subset of 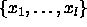sums to t, then the same subset of integers divided by t will sum to 1. Using these divided integers as the sizes for the spec(BP) problem will yield at least one exactly full bin. Since every 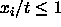, the maximum number of bins needed in the worst case will be l. So, setting k=l will always provide ample bins.

   Validating the reduction in the other direction, if spec(BP) succeeds, then there is at least one exactly full bin. Multiplying the sizes of the objects in this bin by t will yield the corresponding integers in 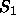which sum to t.

   Thus, SS 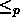spec(BP), and spec(BP) is NP-Hard. Since BP is a more general problem than spec(BP), BP is also NP-Hard.

   The first-fit heuristic takes each object in turn and places it into the first bin that can accommodate it. Let S = .

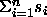   b.

   Argue that the optimal number of bins required is at least .

   Since , the total size S required to store the objects may be non-integral. In the best case the first bins are completely full, and a possible extra bin holds the remaining objects comprising the fractional part of S. Therefore, the total bin space must be the smallest integral size greater than or equal to S, which is .

4. Consider the subgraph isomorphism problem (SI) that takes two graphs and and asks whether is a subgraph of . Prove that SI is NP-Complete by reducing from the clique problem.

   SI: Given two graphs, G = (V1, E1) and H = (V2, E2), there is a subgraph of G that is isomorphic to H; that is, a subset V <= V1 and a subset E <= E1 such that |V| = |V2|, |e| = |E2|, and there exists a one-to-one function f: V2 -> V satisfying {u, v} E2 if and only if {f(u), f(v)} E.

   First prove that SI is in NP.

   The certificate is a subgraph G' of G and a mapping f from G' to H. In time we can verify that the mapping is one-to-one from G' to H.

   Now prove that SI is NP-Hard.
   Reduce CLIQUE to SI.
   Recall that CLIQUE looks for a completely connected subgraph of size >= k.

   For any CLIQUE problem instance we can transform it to an instance of SI by generating a completely connected graph of size k (this requires steps). If there is a subgraph isomorphic to this graph in G, then there is a clique in G.

5. Use the Boyer-Moore-Matching algorithm to implement a grep utility. Grep takes as input a string s and a file f, and returns each line of f that includes an instance of the string s. Send all code, sample files, and compile information to cs5311-turnin@cse.

• About this document ...