CIRCUIT-SAT 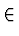is NP-Complete

Proof:

1.

CIRCUIT-SAT $\in$ NP
Proof: Can verify an input assignment satisfies a circuit by computing the output of a finite number of gates, one of which will be the output of the circuit. This can be done in polynomial time. Thus, by definition of NP, CIRCUIT-SAT $\in$ NP.

2.

CIRCUIT-SAT $\in$ NP-Hard
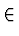I.e., L CIRCUIT-SAT for every L $\in$ NP

Proof: Complex

Show that any problem in NP can be computed using a boolean combination circuit (i.e., a computer).

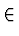This circuit has a polynomial number of elements and can be constructed in polynomial time. Thus, L CIRCUIT-SAT for all L $\in$ NP.

Thus, CIRCUIT-SAT 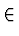$\in$ NP-Hard.

CIRCUIT-SAT is NP-Complete

Proof by Cook, 1971