| Algorithm |
Representation |
Usage |
Adv |
Disadv |
| Association Rule |
Prop if-then |
discover |
simple |
slow, rep, |
| |
|
correlations |
no oracle |
no predict |
| Decision Tree |
Disj of |
prediction |
robust prediction, |
overfit, |
| |
prop conj |
|
symbolic rules |
representation |
| Neural Network |
Nonlinear |
prediction |
numeric, |
overfit, slow, |
| |
numeric f(x) |
|
noisy data |
difficult to |
| |
|
|
|
interpret output |
| Naive Bayes |
Est prob |
prediction |
noisy data, |
not effective |
| |
|
|
provable answer |
in practice |
| Belief Network |
network & CPTs |
prediction, |
prior info, |
slow |
| |
|
variable influence |
prob dist |
learn structure |
| Nearest Neighbor |
Instances |
prediction |
no training, |
slow query, |
| |
|
|
no fixed bias |
redun attributes |
| |
|
|
no loss of info |
no bias |
| Clustering |
clusters |
discover correlations, |
no oracle, |
difficult to |
| |
|
discover var influence |
find similar features |
interpret output |
| |
|
find sim instances |
|
|


- Image-Based Data Mining
- Job posting on Monday
- Analyze images for stroke, aging, trauma
- Newswire Data mining
- Reuters Newswire (1987)
- 22,173 documents
- 135 keywords (countries, topics, people, organizations, stock exchanges)
- Background knowledge: 1995 CIA World Factbook
(member of, land boundaries, natural resources, export commodities,
export partners, industries, etc.)
- Iran, Nicaragua, USA
 Reagan (6/1.0)
Reagan (6/1.0)
- Iran, USA
 Reagan (18/0.692)
Reagan (18/0.692)
- gold, copper
 Canada (5/0.625)
Canada (5/0.625)
- gold, copper
 USA (12/0.571)
USA (12/0.571)
- gold, copper
 Switzerland (5/1.0)
Switzerland (5/1.0)
- gold, copper
 Belgium (5/1.0)
Belgium (5/1.0)
- Churning (customer turnover) in telecommunications industry
- Cost of churn is approximately $400 per new subscriber
- Prediction (will this customer churn and when)
- Understanding (why do particular customers churn)
- Act (reduce churn rate by offering incentives)
- account length in days, international plan, voice mail,
number of messages, length of day time calls, length of evening calls,
length of night calls, length of international calls, customer service calls,
churn status
- Clusters
- International Users (no voice mail, high international usage)
- Internet Users (no voice mail, high day, evening, night usage)
- Busy Workers (no voice mail, low day and evening usage, high
customer service calls)
- Long term customers, long term voice mail customers, new customer



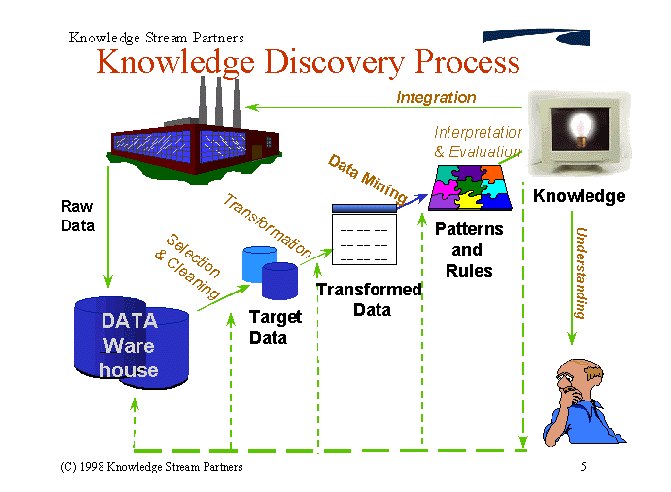


- Convert data to desired format
- Transform data
- Normalization
- Smoothing
- Data Reduction
- Feature discretization
- Sampling
- Feature selection
- Feature composition
- Often requires human assistance to find best set of transformations
- Dealing with Missing Data
A discretization algorithm converts continuous features into
discrete features

- 1.
- Some algorithms are limited to discrete inputs
- 2.
- Many algorithm discretize as part of the learning algorithm,
perhaps not in the best manner
- 3.
- Continuous features drastically slow learning
- 4.
- More easily view data
Discretization can be classified on two dimensions
- 1.
- Supervised vs. unsupervised
Supervised uses class information
- 2.
- Global (mesh) vs. local

One can apply some discretization methods either globally or locally
Here we consider only global discretization of single features.
- 1.
- Limit scope of problem
Allowing discretization of multiple input features is as hard as entire
induction problem
- 2.
- Easy to interpret discretization
- 1.
- Given k bins, divide the training-set range into k equal-size bins

- 2.
- Problems
- (a)
- Unsupervised
- (b)
- Where does k come from?
- (c)
- Sensitive to outliers

- Split into intervals of equal size
- Divide m instances into k bins, each containing m/k(possibly duplicated) values
- This method is unsupervised
- Not often used
A possible local unsupervised method: k-means clustering
- Developed in 1993 by Holte
- Used in OneR induction algorithm
- Induces one-level decision trees (decision stumps)
- Divide range into pure bins
- Each bin contains strong majority of a class
- Each bin must include at least threshold number of instances
- This method is supervised
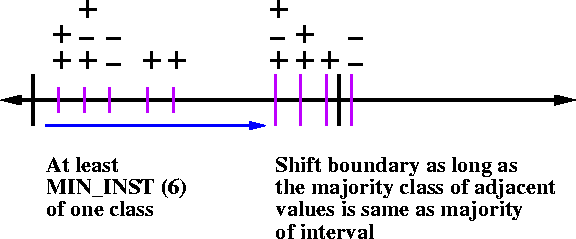
- Developed in 1993 by Fayyad and Irani
- Find best threshold split, such that
mutual information between feature and label is maximal
- Split data according to threshold
- Given
- Set of instances S
- Feature A
- Partition boundary T
- Class entropy of partition induced by T, E(A,T;S) is calculated as
- Recursively discretize each partition
- Stopping condition based on MDL Principle, stop when
where
- N is number of instances in set S
- Gain(A,T;S) = Ent(S) - E(E,A;S)
-

- Run time is
O(km lg m), space is O(m)
How many partitions? D2 (Catlett), MDL approach (Fayyad and Irani) offer
answers.
This method is supervised.
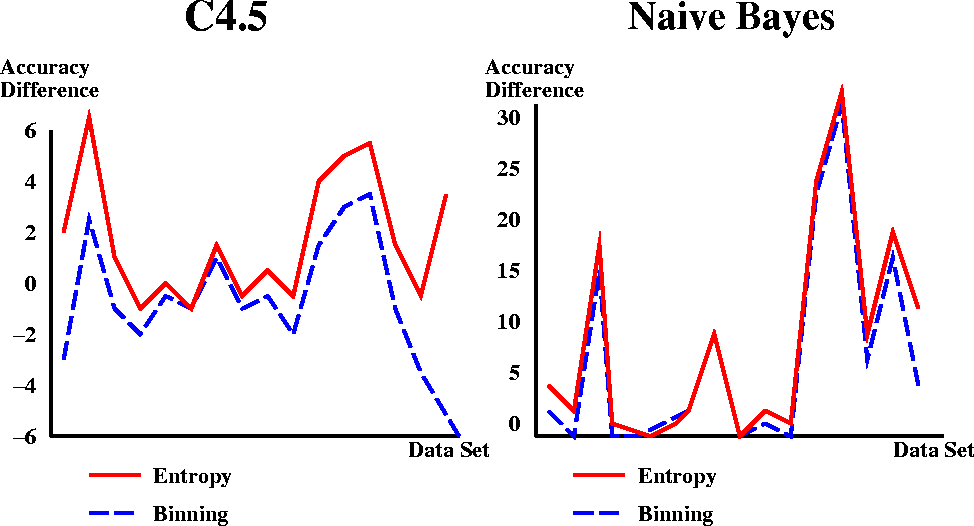
- Compare binning, 1R, and entropy-based partitioning
- Use C4.5 and Naive Bayes with and without discretizations
- Test on 16 UCI datasets, all with at least one continuous feature
- 1.
- Discretize entire data file
- 2.
- Run 10-fold cross-validation
- 3.
- Report accuracy with and without discretization
- 4.
- Why is this bad?
Large differences in number of intervals. Here is result of diabetes dataset.
| Method |
Accuracy |
Intervals per attribute |
| Entropy |
76.04 |
2 |
4 |
1 |
2 |
3 |
2 |
2 |
3 |
| 1R |
72.40 |
6 |
13 |
4 |
6 |
18 |
25 |
41 |
12 |
| Binning |
73.44 |
8 |
14 |
11 |
11 |
15 |
16 |
18 |
11 |
- All discretiation methods for Naive Bayes lead to average increase
in accuracy
- Entropy improves performance on all but three data sets
- C4.5, not much change
- Similar to Entropy method
- Use C4.5 to build a tree with just the one continuous feature
- Apply pruning to find appropriate number of nodes
(number of discretization intervals)
- Increased pruning confidence beyond default value
- Run time is
O(lg1/(1-p m * m lg m), where p is
portion of instances split with each decision
- Space is O(m)
- How many training examples do we need?
- What type of training examples do we need?
- More training examples, better accuracy
- PAC learning
- Random sampling
- Avoid bias
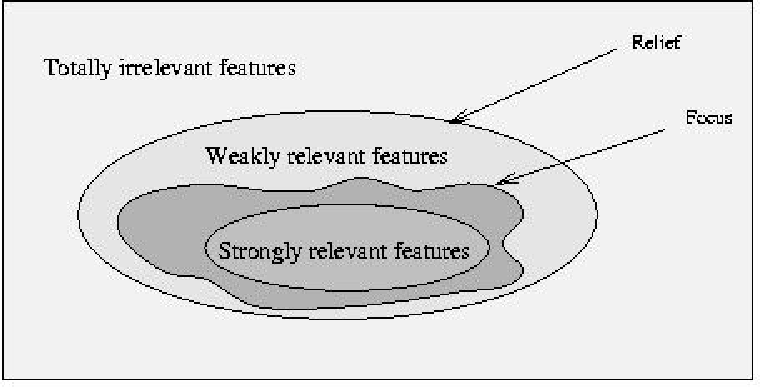
Selecting a subset of features to give to data mining algorithm.
Motivations
- 1.
- Improve accuracy, many algorithms degrade
in performance when given too many features
- 2.
- Improve comprehensibility
- 3.
- Reduce cost and complexity
- 4.
- Investigate with respect to classification task
- 5.
- Scale up to datasets with a large number of features
Credit Approval Database
- Initial number of features: 14
- Criterion: maximal information gain
- Selected features
- Other investments
- Savings account balance
- Bank account
- Conclusion: Other 11 attributes not required for predicting class of
customer
- Bayesian approach: no bad features
- Information-theoretic approach: prefer features which reduce
uncertainty (entropy) in class
- Distance measures: maximize distance between prior and posterior
distributions of class
- Dependence measures: correlation
- Consistency measures: find minimum set of features
- Accuracy measures: choose set of features which maximizes accuracy
Given
- Inducation algorithm I
- Dataset D
The optimal feature subset S* is set of features that yields in
highest-accuracy classifier.
where I(DS') is the classifier built by I from the dataset D using
only features in S'.

- Select features in a preprocessing step
- Generally ignores effects on performance of the learning algorithm
- Almuallim and Dietterich, 1991
- Considers all subsets of features
- Selects minimal subset sufficient to determine label
value of all training instances (MinFeatures bias)
- Does not generalize well
- Example: use SSN as only feature to discriminate people
- Compute mutual information between each feature and class
- MI between two variables
- Average reduction in uncertainty about second variable given value of
first variable
- Assume evaluating feature j
- MI weight wj is
- P(y=c) is proportion of training examples in class c
- P(xj=v) is probability that feature j has value v
- More difficult for real-valued features
- Each feature is treated independently
- Parity function over n features
set all weights W[A] = 0
for i = 1 to m do
randomly select instance R
find nearest hit H and nearest miss M
for A = 1 to AllAttributes do
W[A] = W[A] - diff(A,R,H)/m + diff(A,R,M)/m
Here diff(Attribute,Instance1,Instance2) calculates difference between values
of the Attribute for two instances.
- Discrete attributes: differences is 0 or 1
- Continuous atributes: difference is actual difference normalized
to [0,1] interval
- All weights are in interval [-1,1]
- Generate decision tree using training set
- Decision tree usually only uses subset of features
- Select features that appear in decision tree
- Features useful for decision trees not necessarily useful for
nearest neighbor
- Totally irrelevant features will be removed
- Decision trees do not test more than O(lgm) features in a path
 62
62
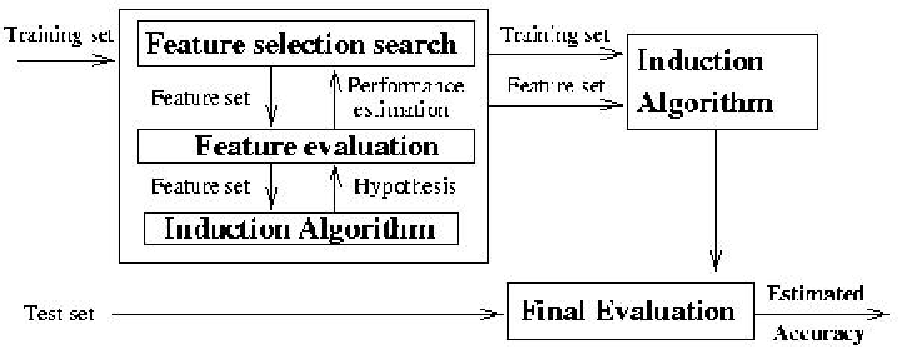
- Kohavi
- Use induction algorithm as a black box
- Conduct search (best-first search here) in the space of subsets
- The estimated prediction accuracy using cross-validation is the
search heuristic
- Tested wrapper using ID3 and Naive Bayes
- Best-first search starting with empty set of features
- Final feature subsets evaluated on unseen test instances using
five-fold cross validation
- Wrapper very slow
- Wrapper has danger of overfitting
- Idea for both approaches: weight features, integrate into ML algorithm
- Used AutoClass class as input feature
- No significant performance improvement
- AutoClass class was root feature in all of the best trees
- AutoClass results used to remove features without significant change
in accuracy
IBM Advanced Scout
http://www.research.ibm.com/scout
- Most prediction methods do not handle missing data well
- Missing values cannot be multiplied or compared
- Solutions
- Use only features with all values
- Use only cases with all values
- These methods lead to bias and insufficient sample sizes
- Fill in missing values during data preparation
- Replace all values with single global constant
- Replace each missing value with a single value (single imputation)
- Replace all missing values with ``unknown category''
- CART uses this approach
- Adds additional parameter to estimate
- Does not reflect fact that missing value is actually part of original
value set
- Can form class just on ``unknown category'' value
- Problem: The replaced values are frequently not the correct value
- Replace a missing value with its feature mean (mean imputation)
- Replace a missing value with its feature and class mean
- Replace by expected value calculated from probability distribution
- Do not capture uncertainty about true value
- Methods can lead to biases
- Replace each missing value by vector of M imputed values
- Generates M complete data sets
- Analyze each set separately
- Pretend missing value has all possible values
- Weight each value according to frequency among examples in that part of
space
| Day |
Outlook |
Temperature |
Humidity |
Wind |
PlayTennis |
D1 |
Sunny |
Hot |
High |
Weak |
No |
| D2 |
Sunny |
Hot |
High |
Strong |
No |
| D3 |
Overcast |
Hot |
High |
Weak |
Yes |
| D4 |
Rain |
Mild |
High |
Weak |
Yes |
| D5 |
Rain |
Cool |
Normal |
Weak |
Yes |
| D6 |
Rain |
Cool |
Normal |
Strong |
No |
| D7 |
Overcast |
Cool |
Normal |
Strong |
Yes |
| D8 |
Sunny |
Mild |
High |
Weak |
No |
| D9 |
Sunny |
Cool |
Normal |
Weak |
Yes |
| D10 |
Rain |
Mild |
Normal |
Weak |
Yes |
| D11 |
Sunny |
Mild |
Normal |
Strong |
Yes |
| D12 |
Overcast |
Mild |
High |
Strong |
Yes |
| D13 |
Overcast |
Hot |
Normal |
Weak |
Yes |
| D14 |
Rain |
Mild |
High |
? |
No |
D14 now becomes
D14 Rain Mild High Weak No (weight = 8/13 = 0.62)
D14 Rain Mild High Strong No (weight = 5/13 = 0.38)
Gain(Wind) = I(9/14, 5/14) - Remainder(Wind)
Remainder(Wind) =
=
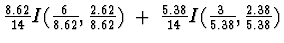
- Working with Honeywell maintenance data
- Database contains 4,383 records, each with 82 features
- No instance is complete
- Only 41 variables have values for more than 50% instances
Methods
Results
- C4.5 yielded 22.6% error rate for target variable
- AutoClass yielded 48.7% error rate for target variable
- Using top three choices, AutoClass error rate was 18%










































![]() nearest instance from different class) -
nearest instance from different class) - ![]() nearest instance from same class)
nearest instance from same class)





 62
62









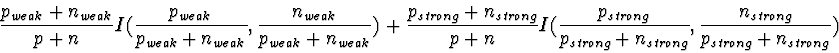
![]()
