


Next:
Up:
Previous:
-
Entropy(S) = expected number of bits needed to encode class (
 or
or
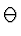 )
of randomly drawn member of S (under the optimal, shortest-length
code)
)
of randomly drawn member of S (under the optimal, shortest-length
code)
Why?
- Information theory: optimal length code assigns
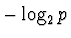 bits to
message having probability p.
bits to
message having probability p.
So, expected number of bits to encode  or
or 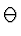 of random member
of S:
of random member
of S:


![]() or
or ![]() of random member
of S:
of random member
of S: