Program design is the development of an algorithm to solve a problem. Algorithms are, as you know, a set of steps to solve a problem in a finite amount of time. By definition, an algorithm is independent of any particular programming language, so a program design must, by implication, avoid relying on the features of a given computer language.
Design is the single most important step in writing any program. When you write your very first programs, they are typically small enough that the importance of design is not readily apparent. Quite often, you can just "see" how to write the few lines of code that it will take to implement the program. As programs get larger, the importance of design becomes easier to understand. Since this is true, it is a good idea to get into the habit of designing, rather than hacking, your programs from the very beginning, even though the design phase may seem like a waste of time to you.
The benefits of designing a program before you start to code it are many. Because designs are typically written in plain English, it is usually faster and easier to write the design than it is to write the code itself. This means that if you find an error in your logic in the design phase, it will be faster to fix than if you find it only once you have coded the algorithm. Sometimes, if you fail to design carefully, thoughtfully, and completely, you will find that you have coded a great deal of a large program only to discover that your original approach suffers from fundamental problems. This generally means that you will have to throw out large portions of the code you have written and start fresh. If you designed the program before writing it, you might have to throw out large portions of your design, but this will cost you much less time!
The process of designing a program also allows you understand ambiguities or incomplete specification of the original problem that you would probably not otherwise discover until you had already written major portions of the program. When you find the parts of the specification that are confusing and ask the client or your teacher for clarification, you may find that your program does not allow you to implement the program as required.
A completed design also provides a means of comparing the specifications and the program function realistically before you start the coding phase. Any program worth writing must do what its specifications require and it must perform those tasks correctly. Because a design is in normal English, it is easier to understand the functioning of the program at this phase than it is in coded form.
A good design will also allow program modification over time. Most programs are not static. That is, they change to incorporate new features, execute more efficiently, or overcome incorrect behavior. A design breaks a large problem into multiple independent or semi-independent parts. These parts become modules that a programmer can reuse in other programs or replace with a similar but more efficient module or with a corrected module. Because the modules are small, they are relatively easy to understand, and therefore easy to debug. Taken individually, they are simple and straightforward to implement. Taken as a whole, they are powerful enough to solve large, complex problems.
When you write a program that is non-trivial, and especially a program that is large, the complexity of the task can be overwhelming. Even a small program can seem to have too many parts for beginning programmers. Quite often, novices feel that they really don't know how to get started. A top down design is the best defense against confusion and chaos. It is a disciplined model for designing programs that allows even the largest programs to be broken into manageable pieces.
A top down design is a plain-English "plan" for the program. We start out thinking about the program in the abstract, that is, we think about the major steps or subtasks in a program. As we refine each of these steps, (we begin to think about the details involved in each subtask) we approach a point at which the algorithm for each of these steps becomes both concrete and easily translatable into a particular programming language. One important point to remember is that a top down design should always be separate from any given programming language. It should never contain references to syntactic elements or library functions peculiar to a certain language. This is why we write top down designs in ordinary English.
The idea behind a top down design is to first divide the work that a program will perform into a small number of broad subtasks. We call this the top level, the main module, or level 0. The number of subtasks at this point should be small. For most programs, we would expect anywhere from about three to six or seven subtasks at this level. For smaller programs, the number of subtasks should be at the low end of this range.
Once we have determined what the major subtasks are for the program as a whole, we have also essentially divided the problem into several smaller (and therefore simpler) programs. It is possible that one or more of these subtasks is already so simple that we can immediately see how to write the code to accomplish it. At level 0, this is usually not the case, however. Whenever a subtask will take more than a very few lines of code to implement it, we need to repeat the process of subdividing. Most often, for each of the subtasks at level 0, we will start a new module at level 1. We take each of these subtasks individually and again divide the work into several subtasks, specifying them as before in plain English. We continue this process of subdividing and creating new levels until it becomes clear how we can implement each part of the problem with computer code.
The result of this method of design is a "tree-like" structure (you will soon
learn that in Computer
Science, trees grow downwards!). Just as the trunk of a tree divides into several large
branches, each large branch divides into smaller branches and each small branch divides
into twigs, the modules at each level of a top down design spawns several modules at the
next level down and each of these gives rise to several more modules at the next level.
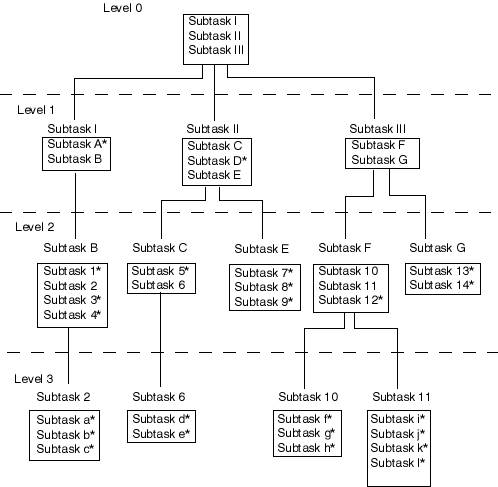
Pictorially, we can depict a top down design as follows:

*These subtasks are already simple enough to be implemented in one or a very few lines of code and thus do not need further expansion.
You will probably understand the principles of top-down design more clearly by means of an example. We will begin with the specifications for a program and then develop a design for the program. A few words of caution are in order before we begin. Students commonly make two mistakes when it comes to designing programs. First, students frequently terminate the design phase too soon. If you cannot look at the description of a subtask and immediately understand exactly what lines of code you will use to implement it, you need to proceed to the next level. At the bottom level, implementation should seem trivial to you. If you stop before this point, you will reap none of the benefits of designing a program, and you will have simply wasted your time. Even with seemingly very simple programs, you will find that you need to go past levels 0 and 1 with surprising regularity. A large program, such as commercial programs, might need hundreds of modules or even more.
The second mistake is to write your design after you have written the program, instead of before. This practice is clearly a waste of time. Programs that you write without designing first are almost always disorganized, inefficient, and not surprisingly, poorly designed! A practiced eye can spot a program written before a design was elaborated without needing to look very hard at all. There are two reasons that so many students write the program first and the design last. First, many students find that they have logic errors in the program even after designing it. This means they must make changes to the program after the design phase, with the consequence that the design and the program don't "match." Avoiding the error of quitting the design phase too soon will mitigate this mismatch, but it will probably not entirely solve the problem. Even with careful design, you may find errors after you have coded the program. You need to realize that it's alright if the final program and the design don't match perfectly. In fact, in a beginning programming class, your teacher will recognize that a design that matches a program exactly is almost certainly a design written after the fact!
In the example below, comments about the development of the design are in green.
Specifications:
Write a program to print the sum of the sum of the digits of each even number in an input file, then to print the smallest number in the file and the largest number in the file. Assume the file contains only positive numbers and that no number is larger than 1000.
The first step is to try to understand what the specifications are asking. In these specification, probably the hardest part to understand is the first part. What does it mean to "print the sum of the sum of the digits of each even number in an input file?" When we read the rest of the specifications, we see a further description of the file, so we begin to envision what the file might look like. Plainly, the file will contain a series of numbers, so it is reasonable to assume that some of these numbers might be even and others odd. Since the first line talks about even numbers, we know that at least here, we will need to ignore any odd numbers the file might contain. The difficult sentence is talking about the digits of the even numbers. At this point, we realize that any given number has one or more digits, so the "sum of the digits" means that we are to add the digits in each even number. It is helpful here to pose an example of an even number with several digits, such as 374. The sum of the digits in this number, then, is 3 + 7 + 4 = 14. Now, let's imagine that the file contains four even numbers. If we sum the digits of those four numbers, we will have four different results (sums). Again, using a concrete example will help us to understand the problem. Let's suppose we find the following even numbers in the file, along with the results of summing their digits:
| number | digit sum |
| 374 | 14 |
| 128 | 11 |
| 2 | 2 |
| 4696 | 25 |
By now it should be clear that the "sum of the sum of the digits" means that we should add the numbers in the "digit sum" column. The rest of the specifications are reasonably clear. As we read the numbers in the file, we will need to keep track of the smallest and the largest numbers we have seen so far, so that we can print these numbers out at the end. We are ready to start designing.
Design:
Level 0:
Main module 1. initialize variables 2. for each number in the input file repeat steps 3-6 3. determine if the number is odd or even; if even do steps 4 and 5, 4. sum the digits of the number 5. add the digit sum to the total sum 6. determine if a new smallest or largest number has been found 7. print the results
After writing the steps in the main module, only steps 5 and 7 are sufficiently simple for us to "see" what the lines of code will need to be that will implement the steps. This means that we need to expand the other steps at another level:
Level 1:
Initialize Variables
1. set the largest number to 0 This means that any number in the file will be larger than the initial value 2. set the smallest number to 1000 any number in the file will be smaller than this initial value 3. initialize the input file for reading 4. set the total sum to 0
Determine if the number is odd or even
1. get the remainder that results from dividing the number by two 2. if the remainder is 0, the number is even, otherwise the number is odd
The next module is probably the most difficult to design, so notice that the design defers the "hard parts" until later. This allows us to concentrate on the module as a whole, rather than getting lost in details.
Sum the digits of the number
1. initialize the digit sum to 0 2. as long as the number is not 0, repeat steps 3-4 3. get the next digit and add it to the digit sum 4. eliminate the digit
Determine if a new smallest or largest number has been found
1. compare the new number to the largest number so far; if it is greater,
set the largest so far to the new number
2. compare the new number to the smallest number so far; if it is less,
set the smallest so far to the new number
Although you have not yet seen all the programming constructs necessary to implement everything in the modules at level 1, by the time you have learned about repetition and selection in C, you will realize that most of the subtasks in the level 1 modules are sufficiently simple that it will take only one or two lines of code to implement, The only exceptions are the subtasks in the "sum the digits" module. This means we still need another level.
This is the "hard part" of the program, and this is where creative thinking comes into play. One initial approach which seems attractive is to think about reading the numbers one digit at a time, as characters. We know that characters are actually represented as character codes, so it seems possible to find a way to convert from a character code to the numeric equivalent of each digit. In fact, since we know that the digits form an ordered sequence within the character set, it is relatively easy to see that if we subtract the code for '0' from the code for any digit, we will derive its numeric value.
A little further thought, however, will lead us to discard this idea. The problem is that we must perform some mathematical computations on the numbers as a whole, We must be able to determine if each number is odd or even, and we must also be able to compare each number to the largest so far and the smallest so far. If we read the numbers as a series of characters, we have lost their values as integers and we can't perform these operations. If we had not designed the program, but had just started writing it, we might well have already written the code to read the numbers as sequences of characters, to sum the digits and the sum of sums before we realize this fact.
At this point, we would have two choices: first, we could try to "patch" things. For instance, we could add code to determine if a number is even by checking to see if its least significant digit is even. Then we would need to write some more code to close the file, reopen it and then read the entire file again, this time as numbers, so that we could find the smallest and largest numbers in the file. If we do this, we will end up with a disorganized and inefficient program which requires more code, more time, and more debugging. The second choice is to throw out the code we have already written and go back to the "drawing board." This is the better choice by far, but most people are extremely reluctant to throw out code, so most people will make the first (and worst) choice. With either choice, we have wasted time and effort.
On the other hand, since we are still in the design phase, we are still free to find an efficient way to solve the problem. The answer lies in the notation we use for numbers. Each digit or "place" represents a factor to be multiplied by a power of 10. The "one's place" is multiplied by 100, the "ten's place" by 101, the 100's place by 102, etc. This insight leads us in the right direction. What will we get if we find the remainder after dividing any number by 10? The answer is that we will get the "one's place" value. What do we get if we find the quotient of dividing by 10? Obviously, we get a number that has all the places except the "one's place." The remainder gives us the "next digit" mentioned above, and the quotient allows us to "eliminate the digit." It is likely that when we wrote the design for the module, we were thinking of going from left-to-right, whereas this method of extracting digits will cause us to work from right-to-left. Since addition is commutative, however, it won't matter at all in terms of the result. Now, the modules at the final level are trivial:
Level 2:
Get the next digit
get the remainder that results from dividing the number by 10
Eliminate the digit
divide the number by 10