


Next: Impedance Boundary Conditions
Up: Material Modeling
Previous: Material Modeling
In 1990 Luebbers et al. published the first frequency dependent
FDTD formulation [85] by using a recursive convolution
(RC) scheme to model Debye media. They did this by relating the
electric flux density to the electric field through a convolution
integral, discretizing the integral as a running sum, and assuming the
susceptibility function is described by a decaying exponential.
Independently, in 1991 Bui et al. [86] also developed
a RC FDTD model for modeling Debye media. Luebbers et al.
[87] modified the frequency dependent RC formulation to
study wave propagation in a Drude material and soon thereafter
generalized their RC approach to treat M-th order dispersive media
[88]. The approach requires storage of 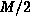 complex
variables per electric field location, while the original scheme for a
first-order Debye media required storage of M real numbers. In
1992, Hunsberger et al. [89] extended the RC
FDTD approach to model an anisotropic magnetoactive plasma, while in
1993, Luebbers et al. [90] formulated a
scattered-field frequency dispersive method and applied it to 3-D
spheres. In 1994, Pontalti et al. [91]
independently proposed an RC approach which could handle Debye media
of M-th order. More recently, Melon et al. [92]
have extended the frequency dispersive RC FDTD approach to ferrite
material. Applications of the FDTD RC include Sullivan's modeling of
3-D biological problems [93] and Hum et al.'s
[94] experimentally verified model of a cylindrical cavity
composed of Debye media.
complex
variables per electric field location, while the original scheme for a
first-order Debye media required storage of M real numbers. In
1992, Hunsberger et al. [89] extended the RC
FDTD approach to model an anisotropic magnetoactive plasma, while in
1993, Luebbers et al. [90] formulated a
scattered-field frequency dispersive method and applied it to 3-D
spheres. In 1994, Pontalti et al. [91]
independently proposed an RC approach which could handle Debye media
of M-th order. More recently, Melon et al. [92]
have extended the frequency dispersive RC FDTD approach to ferrite
material. Applications of the FDTD RC include Sullivan's modeling of
3-D biological problems [93] and Hum et al.'s
[94] experimentally verified model of a cylindrical cavity
composed of Debye media.
While Luebbers and others were developing the frequency dispersive RC
FDTD method, several other researchers were developing an alternate
frequency dispersive method termed the auxiliary differential equation
(ADE) method. The first papers utilizing this approach were by
Kashiwa and co-workers [95,96,97] in
1990 for Debye media, Lorentz media, and media obeying the Cole-Cole
Circular Arc law, respectively. While this research was progressing,
Joseph et al. [98] independently developed a
similar ADE model for Debye media. Goorjian and Taflove
[99] soon extended this model to include effects for
nonlinear dispersive media. Independently, a third research group
headed by Gandhi proposed the ADE method for treating M-th order
dispersive media [100,101]. An approach similar to
the ADE method for modeling the dispersive ionosphere was developed by
Nickisch and Franke [102] in 1992. Additional FDTD
modeling of wave propagation in a plasma using the joint equations of
Euler and Maxwell was developed by Young [103].
The disadvantage of the ADE approach is that it requires storage on
the order of 2M-1 additional real variables, nearly twice that of
the RC method. However, recent research has shown how to reduce this
storage requirement. For example, state-space variable approaches by
Pereda et al. [104] and Young [105] have
reduced the storage of the frequency dispersive ADE method to a level
similar to that of the RC approach.
While the major thrust of FDTD modeling of frequency dispersive media
has utilized either the RC or ADE approach, in 1992 Sullivan
[106] proposed a dispersive formulation based on
Z transforms. Recently, Sullivan [107] has extended
the Z transform approach to treat nonlinear optical phenomena.
Finally, a comparison of the stability and phase error of some
frequency dispersive FDTD methods was provided by Petropoulos
[108].



Next: Impedance Boundary Conditions
Up: Material Modeling
Previous: Material Modeling
John Schneider
Sun Jan 14 12:00:08 PST 1996
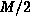 complex
variables per electric field location, while the original scheme for a
first-order Debye media required storage of M real numbers. In
1992, Hunsberger et al. [89] extended the RC
FDTD approach to model an anisotropic magnetoactive plasma, while in
1993, Luebbers et al. [90] formulated a
scattered-field frequency dispersive method and applied it to 3-D
spheres. In 1994, Pontalti et al. [91]
independently proposed an RC approach which could handle Debye media
of M-th order. More recently, Melon et al. [92]
have extended the frequency dispersive RC FDTD approach to ferrite
material. Applications of the FDTD RC include Sullivan's modeling of
3-D biological problems [93] and Hum et al.'s
[94] experimentally verified model of a cylindrical cavity
composed of Debye media.
complex
variables per electric field location, while the original scheme for a
first-order Debye media required storage of M real numbers. In
1992, Hunsberger et al. [89] extended the RC
FDTD approach to model an anisotropic magnetoactive plasma, while in
1993, Luebbers et al. [90] formulated a
scattered-field frequency dispersive method and applied it to 3-D
spheres. In 1994, Pontalti et al. [91]
independently proposed an RC approach which could handle Debye media
of M-th order. More recently, Melon et al. [92]
have extended the frequency dispersive RC FDTD approach to ferrite
material. Applications of the FDTD RC include Sullivan's modeling of
3-D biological problems [93] and Hum et al.'s
[94] experimentally verified model of a cylindrical cavity
composed of Debye media.