In some of the first FDTD calculations of the radar cross section of discrete scatterers, harmonic illumination was used to determine equivalent electric and magnetic currents over a surface that bound the scatterer [134,7,135]. These currents were then transformed to the far-field. An alternative far-field transformation for harmonic illumination was presented in 1991 by Lee et al. [136]. However, by using harmonic illumination in this way, a different simulation had to be run for each frequency of interest. Alternatively, as shown by Furse et al. [137], results could be obtained over several frequencies by using pulsed illumination and a Fourier transform of the equivalent surface currents. These approaches were not well suited for the determination of the temporal far fields. In 1989, Britt [138] presented temporal far-field results, but the means by which he obtained these results were not fully described. Therefore, it was not until the independent work of Yee et al. [139], Luebbers et al. [140], and Barth et al. [141] that efficient 3-D, time-domain, near-field to far-field transformations were developed and described in detail. Luebbers et al. [142] also proposed an efficient 2-D, time-domain, near-field to far-field transformation. Barth et al. [141] and Shlager and Smith [143,144] have also proposed full time-domain near-field to near-field transformations for use with the FDTD method.
Other types of transformations are used in FDTD modeling in order to make the algorithm more efficient. By using digital signal processing techniques, relevant data (such as frequency-domain scattering parameters) can be extracted from FDTD simulations of shorter duration than would otherwise be possible. Ko and Mittra [145], Pereda et al. [146], and Naishadham and Lin [147] have all used Prony's method in this manner, while Houshmand et al. [148], Huang et al. [149], Craddock et al. [150], and Kumpel and Wolff [151] have used the system identification method. Bi et al. [152] have used digital filtering and spectral estimation techniques to improve the FDTD method for eigenvalue problems. Finally, Jandhyala et al. [153,154] and Chen et al. [155] have recently employed autoregressive methods to reduce FDTD computation time.
Analysis of 2-D scatterers illuminated by a 3-D source is possible
using a 2-D FDTD grid. This so-called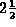 
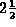-D formulation,
put forward by Moghaddam and co-workers [156],
[157], uses sine and cosine transforms to reduce the
inherently three-dimensional problem to 2-D; however, the full
temporal solution must be constructed from the linear superposition of
several transformed field components.