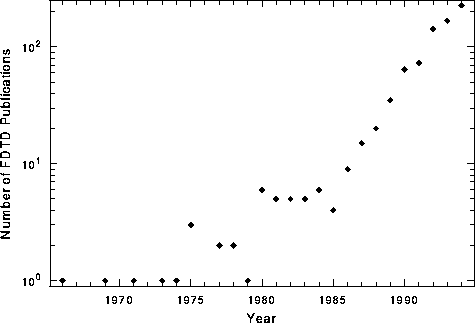
The Finite-Difference Time-Domain (FDTD) method, as first proposed by Yee in 1966 [1], is a simple and elegant way to discretize the differential form of Maxwell's equations. Yee used an electric field (E) grid which was offset both spatially and temporally from a magnetic field (H) grid to obtain update equations that yield the present fields throughout the computational domain in terms of the past fields. The update equations are used in a leap-frog scheme to incrementally march the E and H fields forward in time. Despite the simplicity and elegance of Yee's algorithm, it did not receive much interest immediately after its publication. One could attribute the lack of attention to the high computational cost of the day as well as to some of the limitations inherent in the original publication (such as the inability to model an ``open'' problem for any significant period of time). However, as the shortcomings of the original FDTD implementation were alleviated and the cost of computing fell, the interest in the FDTD method began to soar. In fact, based on the information we have gathered, the number of publications related to the FDTD method has, as shown in Fig. 1, experienced nearly exponential growth in the past ten years.

Since the body of FDTD literature is so large, this survey paper is necessarily incomplete. Therefore, the goal of this paper is merely to highlight some of the more successful extensions to and applications of the FDTD method. Those interested in further exploring the FDTD literature are directed to the on-line database described in Sec. xv.