
Distribution Network Optimization
The distribution optimal power flow (D-OPF) models have gained attention in recent years to optimally operate a distribution grid. The key requirement of the D-OPF is to obtain a feasible solution for the real-time operation in the distribution system. The objective of this work is to propose computationally tractable algorithms for D-OPF.
The figure below gives the overall architecture for power distribution system optimization strategies.
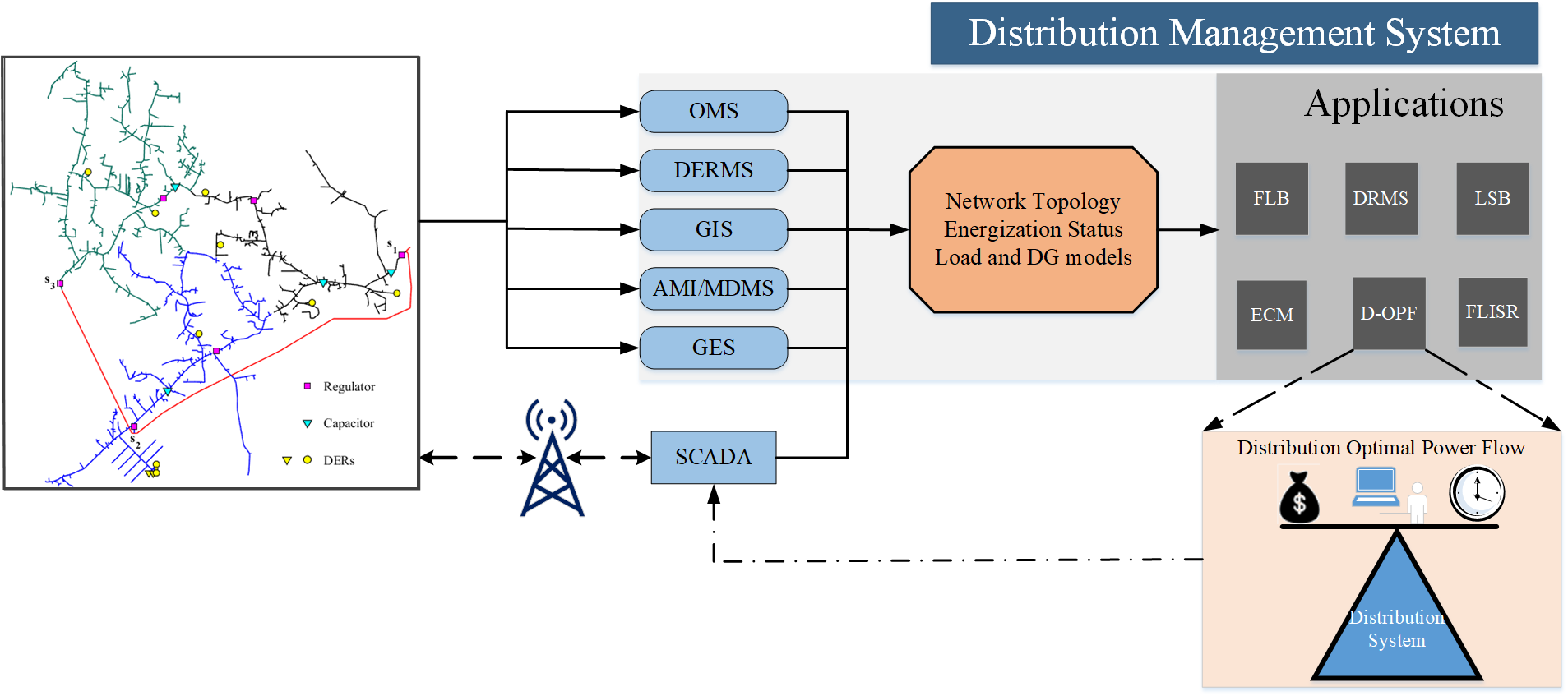
We have worked on three different levels of optimization techniques in the distribution system.
Centralized Control:
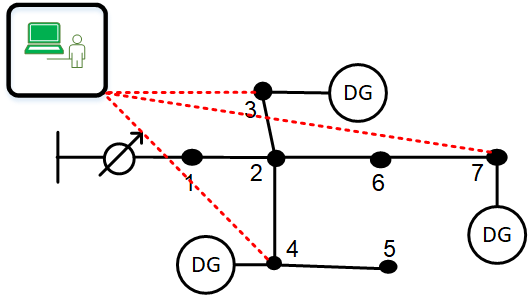
Here, D-OPF formulation is proposed using valid linear and nonlinear power flow approximations for both equivalent single-phase and three-phase unbalanced electric power distribution system.
We have solved the problem in two steps. In the first step, we have modeled the problem as mixed integer linear program (MILP) to control the legacy devices (capacitor banks and voltage regulators) and sectionalizing or tie line switch.
In step-2, nonlinear Program (NLP) is solved with continuous control variables. As the problem is non-convex, the computational time is not adequate for a real-time operation of a large three-phase unbalanced feeder.
In order to improve computation time, low complexity iterative algorithms are proposed via relaxation and approximations of power flow equations.
Specifically, we propose two new methods:
(1) an iterative penalty successive linear program (PSLP) that solves multiple iterations of linear programming problem, and
(2) an iterative second-order cone program (SOCP) that solves multiple iterations of a SOCP to obtain an optimal and feasible solution.
The proposed methods are implemented for several objective functions such as loss minimization, conservation voltage reduction, PV hosting capacity etc.
The proposed methods are tested on equivalent single-phase and three-phase unbalanced test feeder.
Local Control:
For the centralized control, the communications between each controllable device with control center is in discrete time-intervals; it is assumed that system conditions do not change within the discrete decision intervals.
However, due to generation variability introduced by distributed energy resources (DERs), the system conditions change rapidly which may lead to sub-optimal system operation.
We proposed methods where the centralized and local control coordinate with each other to obtain the optimal operation of a distribution system.
We have proposed three local control methods namely Thevevnin’s impedance based methods, power flow measurement based method and adaptive droop curve based methods.
All these local control methods require change in nodal voltage and change in active power injected by the DERs which are available locally.
The implementation of these control techniques is done on the GRIDAPPS-D platform developed at PNNL. The implementation details are below:
Distributed Control:

A centralized operational paradigm requires communication between the Energy Management System (EMS) and all the assets in the power distribution system.
However, a distributed operation relaxes the need for communication between the central control center (EMS/ADMS) and all connected controllable/non-controllable assets.
It improves the overall security and also reduces the computational requirements on a single decision-making unit by distributing the problem to edge computing resources.
Especially when a large number of DERs are present in the system, the computational complexity grows exponentially for a centralized management system.
A distributed approach that solves several instances of smaller sub-problems is typically computationally more efficient.
For Distributed Optimization, we propose a novel distributed algorithm- ‘’Augmented Load Assumption Distributed Optimization Method’’ (ALADOM), based on Block Coordinate Method (BCM).
This Algorithm is 100 times faster than the currently existing method for the power distribution system.